In dit blog gaan we in op hoe je een lineaire regressie uitvoert in R. We illustreren dit aan de hand van een voorbeeld.
Inhoud van dit blog
- Lineaire regressie vs. logistische regressie
- Lineaire regressie Stap 1: Dataset uitlezen
- Lineaire regressie Stap 2: Aannames
- Lineaire regressie Stap 3: Visualiseren met scatterplot
- Lineaire regressie Stap 4: Uitvoeren van lineaire regressie
- Lineaire regressie Stap 5: Interpretatie van resultaten
- Lineaire regressie Stap 6: Visualiseren van voorspellingen
Lineaire regressie vs. logistische regressie
Lineaire regressie behoort tot de methoden die worden gebruikt om toekomstige uitkomsten te voorspellen op basis van beschikbare gegevens. Dit doe je door het samenstellen van een model. Met behulp van statistiek is de kracht/bruikbaarheid van een model te beoordelen.
In onderstaande afbeelding kun je zien welke plaats lineaire regressie inneemt tussen andere statistische algoritmes.
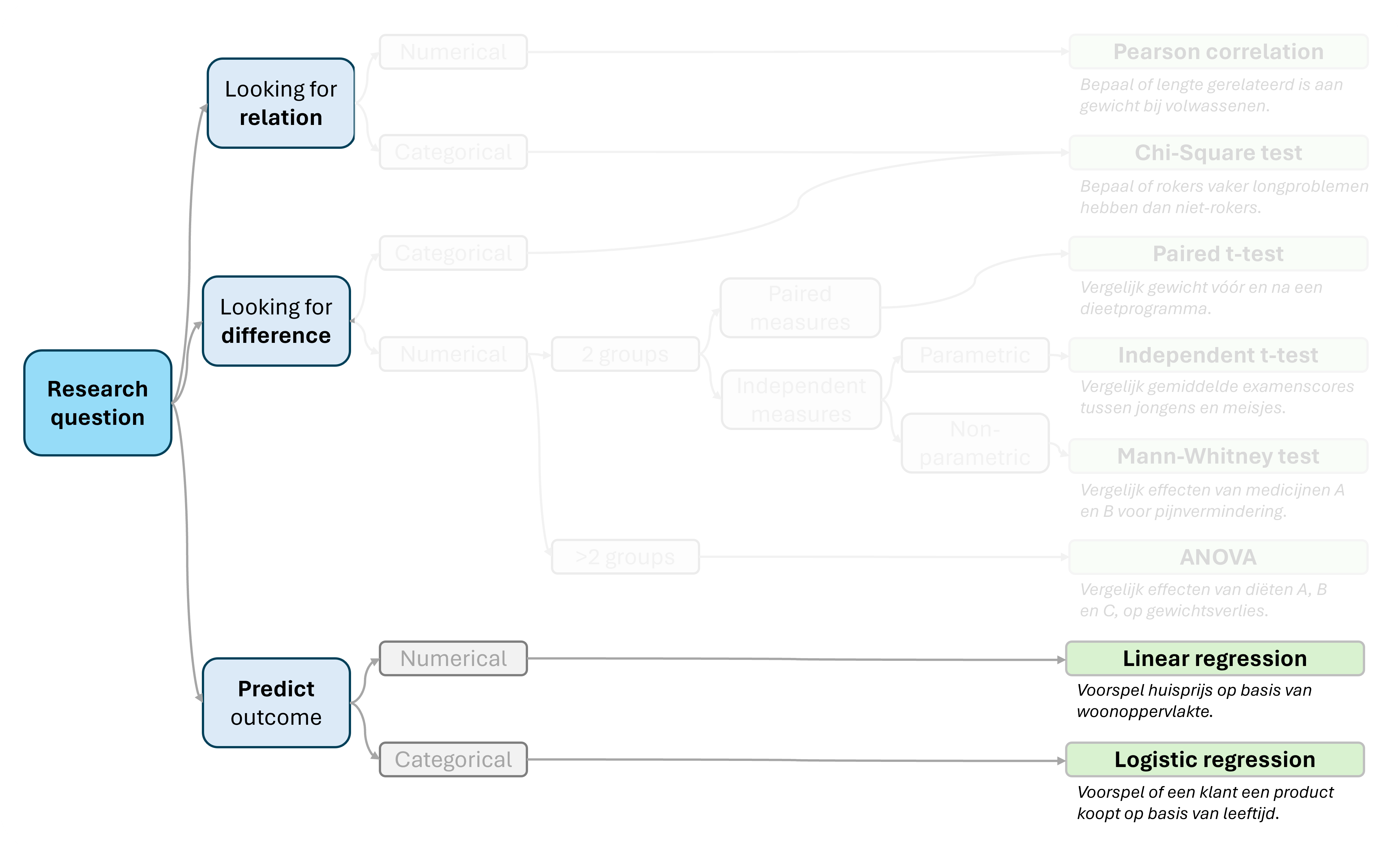
- Lineaire regressie is een statistische methode om de relatie tussen een afhankelijke variabele (uitkomst) en één of meer onafhankelijke variabelen (voorspellers) te onderzoeken. Het doel is om een lineair model te vinden dat de relatie tussen variabelen beschrijft. Bijvoorbeeld het modelleren van de relatie tussen reclame-uitgaven en verkoopcijfers.
- Logistische regressie is een statistische techniek die wordt gebruikt om de kans te voorspellen van een binair resultaat (bijvoorbeeld ja/nee, geslaagd/ongeslaagd), op basis van één of meer voorspellende variabelen. Het model berekent de kans op een bepaald resultaat met behulp van een logistische functie. Denk hierbij bijvoorbeeld aan het voorspellen of een hartaandoening zich ontwikkelt. Op basis van risicofactoren zoals leeftijd, geslacht, BMI, bloeddruk, cholesterol-niveaus.
In dit artikel gaan we dieper in op lineaire regressie in R.
Lineaire regressie Stap 1: Dataset uitlezen
We gaan een CSV bestand uitlezen. Als je mee wilt doen kun je het bestand hier downloaden.
Dit met data van een toets-scores van studenten.
Het bevat de volgende kolommen:
gender: Geslacht van studenten.
iq_score: IQ score van studenten.
study_hours: Studietijd van studenten voor de toets.
test_score: Toets-score van studenten.
df_student_scores <- read.csv("data/students_test_scores.csv")
We gaan aantonen of er een relatie is tussen het IQ, en de toets-score.
Lineaire regressie Stap 2: Aannames
Enkele aannames voor het gebruik van een eenvoudige lineaire regressie:
- Lineair verband: Relatie tussen variabelen is rechtlijnig.
- Onafhankelijke observaties: Waarnemingen mogen elkaar niet beïnvloeden.
- Homoscedasticiteit: Gelijke spreiding van voorspellingsfouten.
- Normaal verdeelde fouten: Fouten volgen normale verdeling rond voorspelde waarden.
Lineaire regressie Stap 3: Visualiseren met scatterplot
Met een scatterplot (puntenwolk) kunnen we de datapunten visualiseren.
We gebruiken package ggplot2 en functie geom_point():
library(ggplot2)
ggplot(
data = df_student_scores,
aes(x = iq_score, y = test_score)
) +
geom_point() +
labs(
x = "IQ score",
y = "Test score",
title = "IQ Score versus Test Score"
)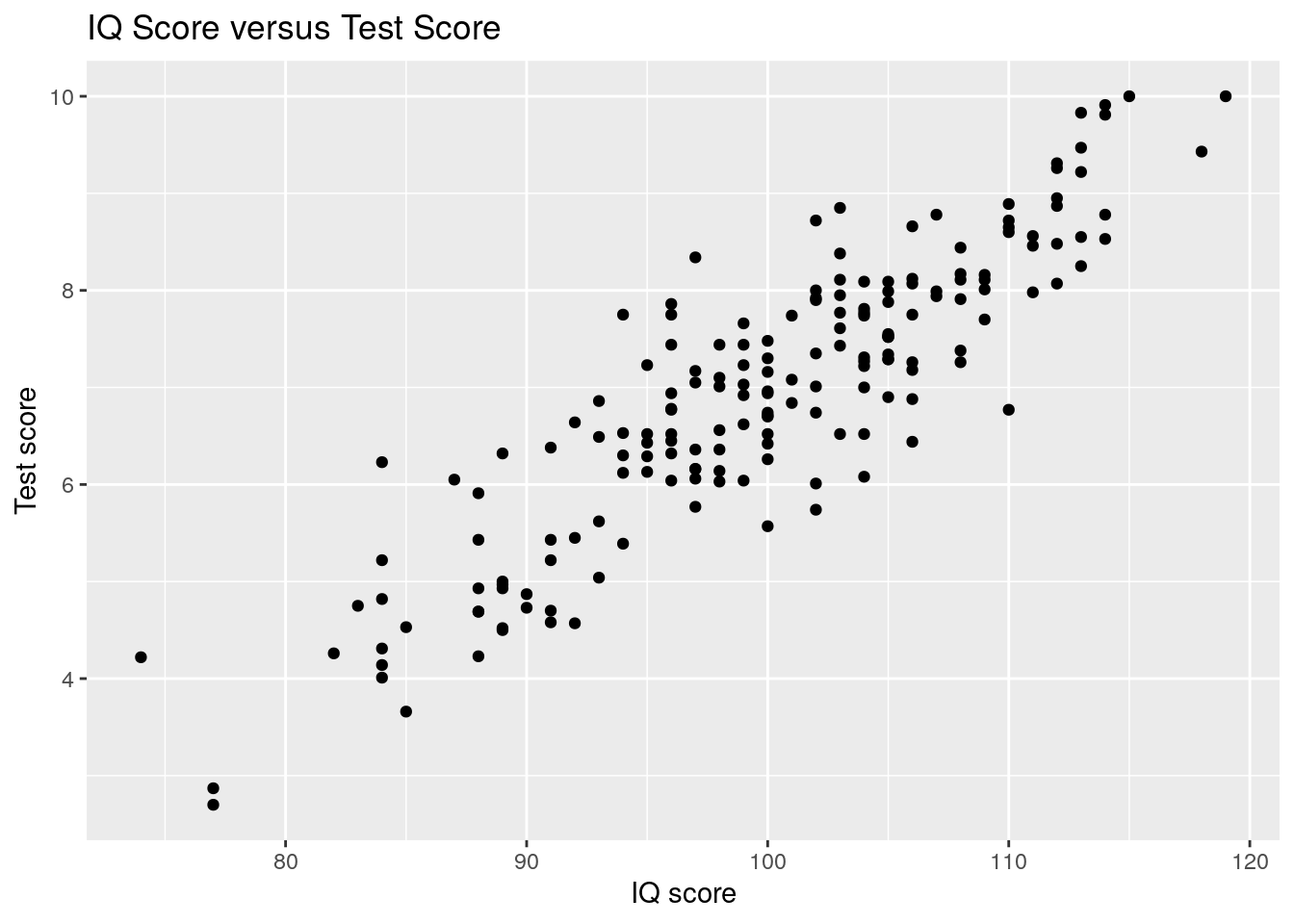
Grafisch is een lineaire relatie te zien: Hoe hoger het IQ, hoe hoger de toets-score.
Lineaire regressie Stap 4: Uitvoeren van lineaire regressie
Nu we onze data hebben geladen, kunnen we de lineaire regressie uitvoeren.
Dit met behulp van de standaard functie lm() (linear model).
- Met
set.seed()verzekeren we reproduceerbaarheid. - Met
formula = test_score ~ iq_scoregeven we de relatie tussen kolommen op. - Met functie
summary()verkrijgen we de uitkomsten van de lineaire regressie.
set.seed(123)
lm_model <- lm(formula = test_score ~ iq_score, data = df_student_scores)
summary(lm_model)##
## Call:
## lm(formula = test_score ~ iq_score, data = df_student_scores)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.66399 -0.42565 -0.03422 0.42364 1.83126
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.856552 0.570270 -13.78 <2e-16 ***
## iq_score 0.148096 0.005688 26.04 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6635 on 180 degrees of freedom
## Multiple R-squared: 0.7902, Adjusted R-squared: 0.789
## F-statistic: 678 on 1 and 180 DF, p-value: < 2.2e-16De uitvoer bevat informatie over het regressiemodel, waaronder:
- De helling (coëfficiënt)
- Intercept
- R-kwadraat (R-squared) waarde
- p-waarde voor de regressiecoëfficiënt
Lineaire regressie Stap 5: Interpretatie van resultaten
We bekijken hier in het kort enkele belangrijke resultaten.
R-squared
Multiple R-squared: 0.7902, Adjusted R-squared: 0.789 R-squared geeft aan hoeveel variatie van een uitkomst-variabele verklaard kan worden door een input-variabele van een regressie-model.
Hierdoor is het een maat voor de nauwkeurigheid van de voorspellende kracht van het model.
In geval van eenvoudige lineaire regressie gebruik je doorgaans de Multiple R-squared metric.
- Dit is hier gelijk aan 0.7902.
- 79% van de variatie wordt verklaard door het model.
- Dit is een sterke relatie.
Coeffcients
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.856552 0.570270 -13.78 <2e-16 ***
iq_score 0.148096 0.005688 26.04 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1We willen een gegeneraliseerd model bouwen in de vorm van y = ax + b.
- Waarbij b het snijpunt (intercept) is van de lijn met de y-as.
- En a de helling (slope) is van de lijn.
(Intercept)is het snijpuntiq_scoreis de helling van de lijn (let op, afhankelijk van gekozen variabele).
Dit geeft de volgende formule: y = 0.148096x - 7.856552
Lineaire regressie Stap 6: Visualiseren van voorspellingen
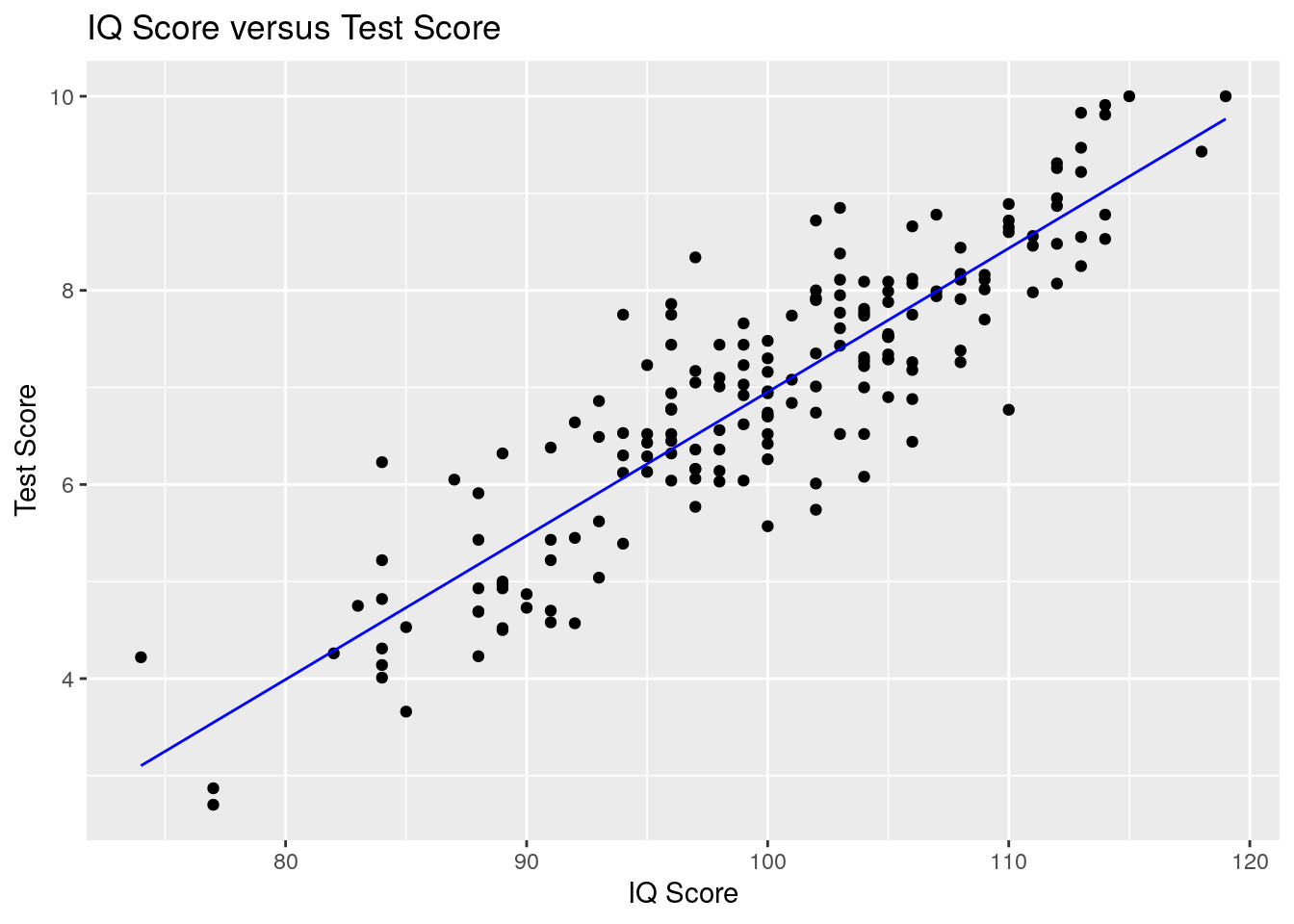
We kunnen aan de eerder gemaakte scatterplot voorspellingsuitkomsten van het model toevoegen.
- Dit doen we met een lijn met
geom_line(). - Daarbij gebruiken we de
predict()functie om voorspellingen van het model te verkrijgen.
library(ggplot2)
ggplot(
data = df_student_scores,
aes(x = iq_score, y = test_score)
) +
geom_point() +
geom_line(
aes(x = iq_score, y = predict(lm_model)),
color = "blue",
) +
labs(
x = "IQ Score",
y = "Test Score",
title = "IQ Score versus Test Score"
)
Dit blog is onderdeel van onze blogreeks over programmeren in R, de veelzijdige programmeertaal die essentieel is in data science. Of je nu een beginner bent of een ervaren gebruiker, deze serie biedt inzichten en praktische tips voor iedereen. We verkennen de basis met Wat is R? en R installeren, duiken in data manipulatie met dplyr en Data Table package, en onthullen de kracht van visualisatie met ggplot2. Voor een geïntegreerde ontwikkelomgeving, bekijk RStudio, en ontdek hoe R Jupyter Notebook de interactieve programmering verbetert. Verdiep je in de Tidyverse met Tidyverse R en leer over R scripts. Of je nu worstelt met de vraag Is programmeren in R moeilijk?, deze serie heeft voor elk wat wils.
Wil je in 2 of 3 dagen zelfstandig met R leren werken in RStudio?
Wil jij goed leren werken in R? Tijdens onze Opleiding R leer je alles wat je nodig hebt om zelfstandig analyses uit te voeren in R. In deze opleiding kun je kiezen voor een extra dag waarin je alles leert over statistiek met R.

Peter is een ervaren data scientist en python trainer. Na zijn studie aan de Technische Universiteit Delft heeft hij zich altijd bezig gehouden met data en diverse programmeertalen. Peter heeft veel data analyses uitgevoerd en processen geautomatiseerd met Python in productieomgevingen.