Een t-test is een vergelijkingstest. Vergelijkingstests worden gebruikt om te bepalen of er significante verschillen zijn tussen groepen of condities. Deze tests helpen ons om te begrijpen of er een verschil is in gemiddelden of verdelingen. En of deze verschillen waarschijnlijk niet te wijten zijn aan toeval.
In dit blog kijken we naar hoe je t-tests doet in R. Als je meedoet is het handig als je R installeert evenals RStudio.
In dit blog leer je:
- Welke verschillende vergelijkingstests zijn er?
- Introductie voorbeeld-dataset
- Verkennen dataset
- Uitleg en voorbeeld paired t-test
- Uitleg en voorbeeld independent t-test
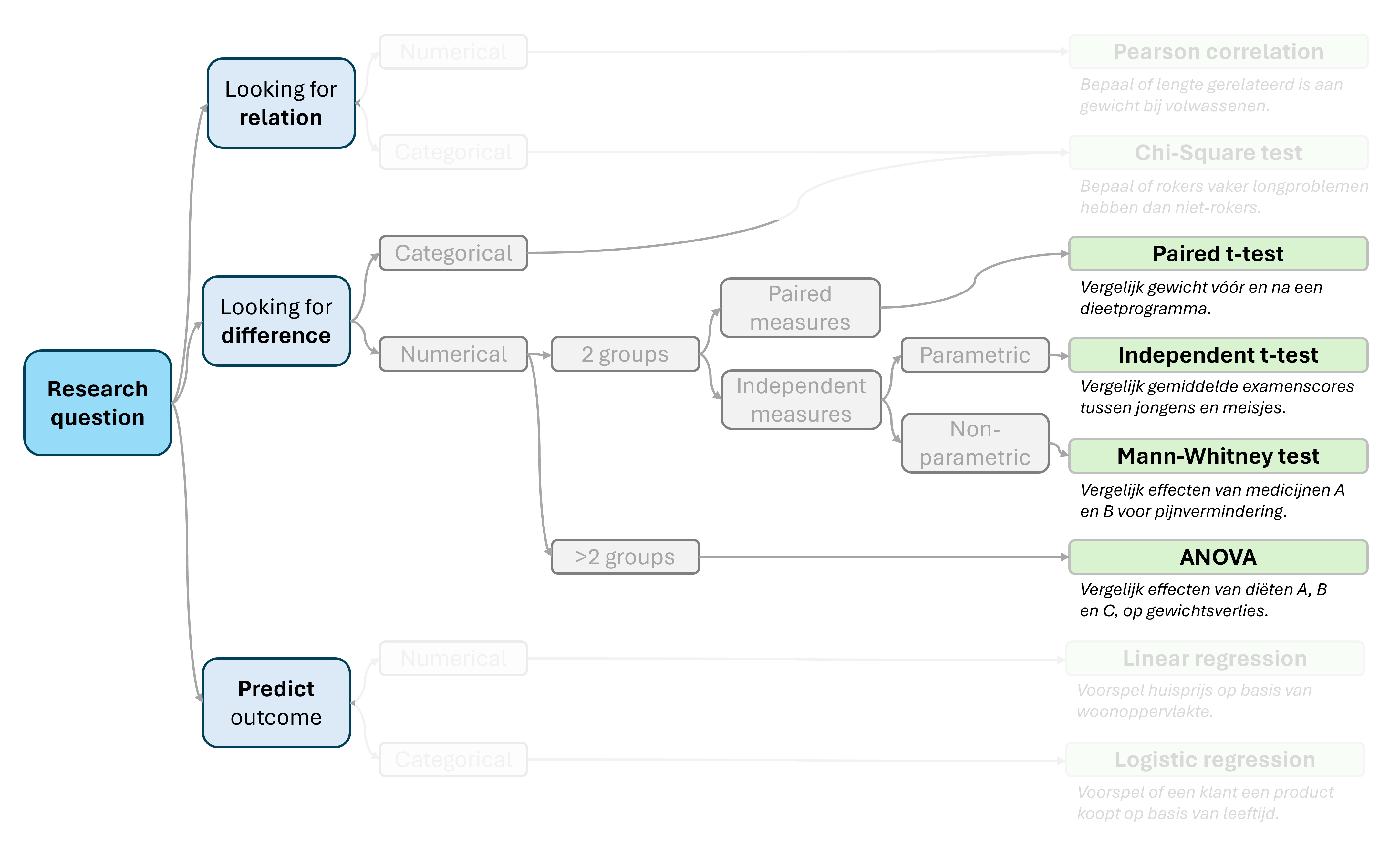
Welke verschillende vergelijkingstests zijn er?
Wanneer je een verschil tussen twee groepen onderzoekt kun je verschillende tests toepassen.
- Een t-test gebruik je om verschil tussen twee gemiddelden te beoordelen. De t-test berekent een t-waarde en een bijbehorende p-waarde. Bijvoorbeeld om te bepalen of er verschil is in bloeddruk vóór en na een medische behandeling. Toe te passen onder diverse aannames. Zoals dat de data normaal verdeeld moet zijn.
- ANOVA (ANalysis Of Variance) gebruik je om verschil tussen drie of meerdere groepen te beoordelen. ANOVA berekent een F-waarde en een bijbehorende p-waarde. Voorbeeld: Om te bepalen of er verschil is in gemiddelde examenscores van vier verschillende onderwijsmethoden.
- Een Mann-Whitney test wordt gebruikt om te bepalen of er een significant verschil is tussen de verdelingen van twee onafhankelijke groepen. Deze test is geschikt wanneer de gegevens niet voldoen aan de aannames van normaalverdeling die bijvoorbeeld vereist zijn voor de t-test. Voorbeeld: Om te bepalen of er verschil is in verkoopcijfers van 2 verschillende producten. Waarbij de data niet normaal verdeeld is.
In deze blog gaan we dus dieper in op de t-test binnen de programmeertaal R.
Introductie voorbeeld-dataset
We gaan een CSV bestand uitlezen met metingen van scores op een toets, vóór en na het volgen van een opleiding. Download paired_test_scores het csv bestand als je mee wilt doen.
Leer meer over uitlezen van csv bestanden in R
df_grades <- read.csv("data/paired_test_scores.csv")
df_grades## grade1 grade2
## 1 5.54 7.19
## 2 5.86 7.13
## 3 5.07 6.85
## 4 5.84 7.53
## 5 5.91 7.14
## 6 5.83 6.97
## 7 6.71 7.03
## 8 5.78 6.84
## 9 5.24 7.40
## 10 6.37 7.32
## 11 6.01 7.02
## 12 6.76 7.15
## 13 5.99 7.47
## 14 5.89 7.14
## 15 6.35 7.00
## 16 6.00 7.41
## 17 5.31 7.14
## 18 5.61 7.14
## 19 5.43 7.43
## 20 6.68 6.96
## 21 5.98 7.28
## 22 6.01 7.28
## 23 6.06 7.14
## 24 6.41 7.21
## 25 6.03 7.26
## 26 5.40 6.72
## 27 6.40 7.42
## 28 6.20 7.01
## 29 5.77 7.67
## 30 5.66 7.10
## 31 6.53 7.39
## 32 5.44 7.55
## 33 6.24 7.07
## 34 5.94 7.43
## 35 6.52 6.77
## 36 6.85 7.11
## 37 6.23 7.18
## 38 5.30 7.37
## 39 5.76 7.02
## 40 5.01 7.35
## 41 5.79 7.03
## 42 5.57 6.79
## 43 5.76 6.81
## 44 5.14 7.27
## 45 6.35 7.09
## 46 6.19 7.54
## 47 6.04 7.35
## 48 5.33 6.99
## 49 5.48 7.15
## 50 6.13 6.95
## 51 6.87 7.06
## 52 5.36 7.29
## 53 6.12 7.00
## 54 6.53 7.16
## 55 5.72 7.49
## 56 6.34 7.20
## 57 6.42 7.50
## 58 5.88 6.87
## 59 5.71 7.36
## 60 5.76 6.89
## 61 5.76 7.24
## 62 5.37 7.10
## 63 6.21 7.16
## 64 6.14 7.31
## 65 4.69 7.13
## 66 6.12 7.22
## 67 6.44 6.89
## 68 5.92 7.26
## 69 6.20 7.48
## 70 5.42 7.31
## 71 6.11 7.21
## 72 6.76 7.17
## 73 5.77 6.90
## 74 6.17 6.59
## 75 6.20 7.30
## 76 6.28 7.05
## 77 5.89 6.97
## 78 5.36 6.85
## 79 5.62 7.10
## 80 6.07 7.35
## 81 6.52 7.11
## 82 5.42 7.35
## 83 6.48 6.91
## 84 6.34 7.18
## 85 5.83 7.27
## 86 6.71 6.92
## 87 6.70 7.44
## 88 7.02 7.31
## 89 5.74 7.39
## 90 7.18 6.83
## 91 6.31 6.96
## 92 5.60 7.19
## 93 6.06 7.14
## 94 5.33 7.08
## 95 6.62 7.21
## 96 7.09 7.11
## 97 5.43 7.04
## 98 6.49 7.51
## 99 6.03 7.05
## 100 6.33 7.11
## 101 5.34 7.28
## 102 5.49 7.32
## 103 6.08 7.44
## 104 5.96 7.40
## 105 6.23 7.07
## 106 6.35 7.37
## 107 5.98 7.21
## 108 5.83 7.49
## 109 5.82 7.30
## 110 5.75 7.14
## 111 6.67 7.14
## 112 6.78 7.20
## 113 5.69 7.19
## 114 7.07 7.31
## 115 6.47 7.43
## 116 6.46 7.30
## 117 6.09 7.42
## 118 5.73 7.23
## 119 6.29 7.55
## 120 6.51 7.28
## 121 5.62 7.35
## 122 5.57 7.27
## 123 5.98 7.25
## 124 5.70 7.43
## 125 6.41 7.07
## 126 6.16 7.27
## 127 5.71 7.20
## 128 6.80 7.38
## 129 5.82 7.27
## 130 6.10 7.57
## 131 5.98 6.88
## 132 5.27 7.31
## 133 6.11 7.41
## 134 5.81 6.91
## 135 6.18 7.36
## 136 5.82 7.34
## 137 5.77 7.16
## 138 5.58 7.55
## 139 7.18 7.14
## 140 5.84 7.14
## 141 5.72 7.52
## 142 5.68 7.13
## 143 5.96 7.58
## 144 5.55 7.02
## 145 7.06 6.99
## 146 5.39 6.97
## 147 6.22 7.25
## 148 5.78 7.66
## 149 6.73 7.30
## 150 6.02 6.97
## 151 5.49 7.33
## 152 6.04 6.89
## 153 6.14 7.29
## 154 6.10 7.35
## 155 6.08 7.01
## 156 5.01 7.06
## 157 5.72 7.30
## 158 6.61 7.34
## 159 5.69 7.09
## 160 6.20 7.24
## 161 6.32 7.03
## 162 6.37 7.29
## 163 6.20 7.35
## 164 5.88 7.10
## 165 6.20 6.96
## 166 5.60 7.20
## 167 6.28 7.24
## 168 5.98 7.02
## 169 5.99 7.38
## 170 5.78 7.17
## 171 5.84 7.50
## 172 6.21 7.38
## 173 6.07 7.28
## 174 4.78 7.00
## 175 5.88 7.28
## 176 6.31 7.28
## 177 6.33 7.35
## 178 6.84 7.18
## 179 5.88 7.22
## 180 6.01 7.33
## 181 6.14 7.26
## 182 5.92 7.41
## 183 5.96 7.53
## 184 6.20 7.09
## 185 6.25 6.97
## 186 5.59 7.19
## 187 6.86 6.95
## 188 6.30 7.29
## 189 6.30 7.05
## 190 5.86 6.90
## 191 5.60 7.18
## 192 6.18 7.52
## 193 6.35 7.16
## 194 5.95 7.11
## 195 5.65 6.93
## 196 6.58 7.43
## 197 6.24 7.16
## 198 6.93 7.26
## 199 7.29 7.36
## 200 5.83 6.95
## 201 5.74 7.01
## 202 5.72 7.31
## 203 5.35 7.30
## 204 5.97 7.06
## 205 6.20 6.94
## 206 5.26 7.27
## 207 6.04 7.22
## 208 5.28 7.36
## 209 5.82 7.02
## 210 6.73 7.25
## 211 5.54 7.45
## 212 6.91 6.98
## 213 6.29 7.05
## 214 5.90 6.86
## 215 5.13 7.10
## 216 6.19 7.30
## 217 6.24 7.27
## 218 5.68 7.29
## 219 6.50 7.29
## 220 6.25 7.12
## 221 6.14 7.27
## 222 6.97 7.40
## 223 6.33 7.26
## 224 6.06 7.28
## 225 4.96 7.21
## 226 5.74 7.23
## 227 5.16 7.39
## 228 5.55 7.28
## 229 5.98 7.28
## 230 7.26 7.08
## 231 5.65 7.29
## 232 6.49 7.21
## 233 6.79 6.83
## 234 5.96 6.96
## 235 6.34 7.23
## 236 6.37 7.19
## 237 6.00 7.63
## 238 6.10 7.05
## 239 5.48 7.45
## 240 6.35 7.16
## 241 5.74 6.93
## 242 7.06 7.26
## 243 6.54 7.51
## 244 5.65 7.03
## 245 5.91 7.12
## 246 4.49 6.85
## 247 5.37 6.97
## 248 5.65 7.31
## 249 5.95 7.12
## 250 6.55 7.30
## 251 6.25 7.26
## 252 6.38 6.80
## 253 6.16 7.07
## 254 6.20 6.92
## 255 5.74 6.98
## 256 6.13 7.35
## 257 6.82 6.96
## 258 5.70 7.19
## 259 5.40 7.40
## 260 5.55 7.24
## 261 5.59 7.26
## 262 5.95 7.26
## 263 6.02 6.97
## 264 7.28 7.03
## 265 5.82 6.98
## 266 5.65 7.15
## 267 5.59 7.50
## 268 5.88 7.18
## 269 6.38 7.09
## 270 6.73 7.47
## 271 5.93 7.12
## 272 6.30 7.22
## 273 5.40 7.27
## 274 6.65 7.32
## 275 6.34 7.50
## 276 5.71 7.05
## 277 6.57 7.23
## 278 6.52 7.10
## 279 6.29 7.12
## 280 6.10 6.95
## 281 5.42 7.12
## 282 5.27 7.36
## 283 5.86 7.26
## 284 5.66 7.46
## 285 5.97 7.06
## 286 6.02 7.05
## 287 6.18 7.46
## 288 5.47 7.38
## 289 6.64 7.41
## 290 5.56 7.34
## 291 5.92 7.17
## 292 5.98 7.24
## 293 5.71 7.08
## 294 5.52 6.85
## 295 6.21 7.18
## 296 6.16 7.56
## 297 5.63 7.29
## 298 6.12 7.47
## 299 5.54 7.39
## 300 5.67 7.21
## 301 6.66 7.30
## 302 7.00 7.10
## 303 6.49 7.23
## 304 5.52 7.03
## 305 5.14 6.93
## 306 6.00 7.72
## 307 6.26 7.24
## 308 5.88 7.19
## 309 6.16 7.15
## 310 6.27 7.21
## 311 5.17 7.15
## 312 5.26 7.13
## 313 5.74 7.44
## 314 6.00 6.96
## 315 5.91 6.79
## 316 5.50 7.18
## 317 6.05 7.22
## 318 7.09 7.09
## 319 6.28 6.93
## 320 6.79 7.34
## 321 5.56 7.04
## 322 5.85 6.98
## 323 6.10 7.42
## 324 6.00 6.89
## 325 5.30 7.23
## 326 7.13 7.32
## 327 5.25 7.19
## 328 5.70 7.19
## 329 5.92 7.28
## 330 6.33 7.14
## 331 6.14 7.24
## 332 6.12 7.40
## 333 6.31 7.45
## 334 5.65 7.01
## 335 5.96 7.03
## 336 5.28 7.05
## 337 6.57 6.99
## 338 6.06 7.05
## 339 5.97 6.97
## 340 7.11 7.35
## 341 5.55 7.11
## 342 5.59 7.19
## 343 6.35 6.88
## 344 6.01 7.25
## 345 5.58 7.28
## 346 6.61 7.23
## 347 5.89 7.39
## 348 6.10 6.97
## 349 5.75 7.34
## 350 5.18 7.32
## 351 6.06 7.34
## 352 6.81 7.05
## 353 6.23 7.45
## 354 6.00 7.16
## 355 5.69 7.17
## 356 5.68 7.12
## 357 6.28 7.05
## 358 6.39 7.23
## 359 6.33 7.19We zien kolommen met score voor het volgen van de opleiding (grade1), en na het volgen van de opleiding (grade2).
We gaan aantonen of er een verschil is in gemiddelde score voor of na de opleiding.
Verkennen dataset
We gaan de dataset wat verkennen in R om een indruk te krijgen van de inhoud.
Gemiddelden berekenen
Met functie sapply() kunnen we de gemiddelden per kolom berekenen.
Dit geeft ons al inzicht in een eventueel verschil.
sapply(X = df_grades, FUN = mean)## grade1 grade2
## 6.018078 7.195042We zien dat het gemiddelde na de opleiding hoger is dan ervoor.
Visualiseren met boxplot
Met een boxplot kunnen we gemiddelden en spreiding van variabelen grafisch weergeven.
Hiervoor hebben we een dataframe nodig met 2 kolommen:
- Categoriale groepsnamen
- Kwalitatieve meetwaaren
Onze dataset voldoet hier niet aan. We hebben nu 2 kolommen met kwalitatieve meetwaarden.
Met onderstaande code gebruiken we functie stack() om de waarden uit de kolommen samen te voegen:
df_grades_stacked <- stack(df_grades)
Vervolgens gebruiken we package ggplot2 om een boxplot te maken:
library(ggplot2)
boxplot_plot <- ggplot(
data = df_grades_stacked,
aes(x = ind, y = values)
) +
geom_boxplot() +
stat_summary(fun = "mean", geom = "point") +
labs(title = "Boxplot of score before (grade1) and after (grade2) training course")
boxplot_plot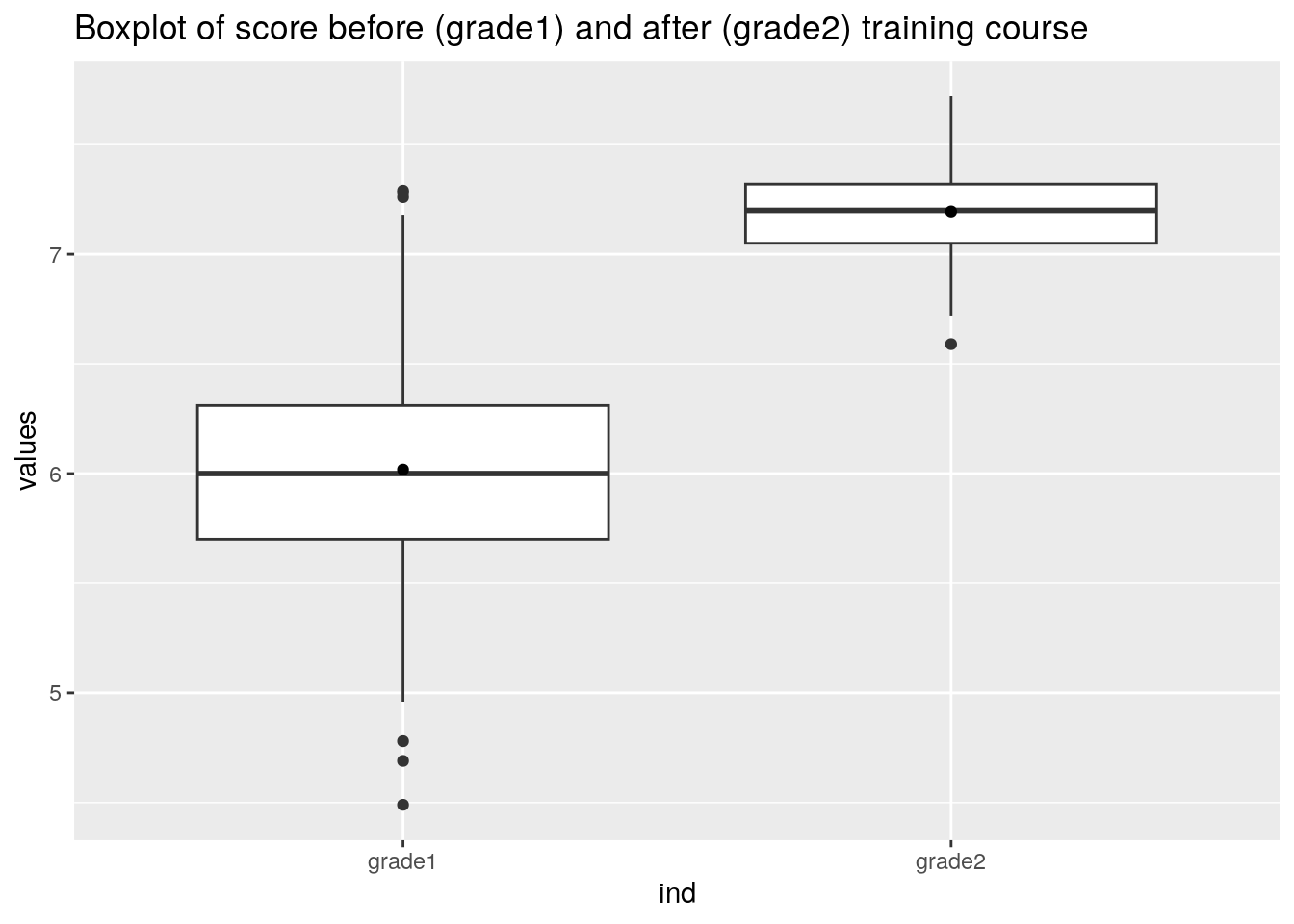
Grafisch is een verschil tussen de scores te zien. We gaan nu onderzoeken of we het verschil ook kunnen bewijzen met een t-test in R.
Uitleg en voorbeeld paired t-test
Een t-test is dus een statistische test die wordt gebruikt om te bepalen of er een significant verschil is tussen de gemiddelden van twee groepen. We zullen leren hoe we de t-test kunnen uitvoeren en interpreteren.
We starten met de paired-sample t-test. Deze t-test vergelijkt gemiddelden van twee gerelateerde (gepaarde) metingen. Voor en na een bepaalde gebeurtenis/situatie.
Er bestaat hiernaast ook:
- De independent t-test: verschil in gemiddelden van 2 onafhankelijke groepen.
- One-sample t-test: verschil in gemiddelde en een bekende waarde.
Aannames paired t-test
Enkele aannames voor het gebruik van een t-test:
- Data is normaal verdeeld.
- Waarnemingen zijn onafhankelijk (niet beïnvloed door elkaar).
- Gelijke spreiding (variantie) tussen groepen.
Berekenen van de paired t-test in R
Nu we onze data hebben geladen, kunnen we de t-test berekenen.
Dit met behulp van de standaard functie t.test().
- We geven de kolomnamen op met
xeny. - Met
paired = TRUEspecificeren we dat het een gepaarde test is.- Metingen voor en na horen bij elkaar.
result <- t.test(x = df_grades$grade2, y = df_grades$grade1, paired = TRUE)
result##
## Paired t-test
##
## data: df_grades$grade2 and df_grades$grade1
## t = 43.155, df = 358, p-value < 2.2e-16
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## 1.123328 1.230599
## sample estimates:
## mean difference
## 1.176964De uitvoer van bevat informatie over de t-test
Dit inclusief bijvoorbeeld de p-waarde, en het verschil in gemiddelden.
Interpretatie van resultaten
Laten we de resultaten van de t-test interpreteren.
Dit om te bepalen of er een significant verschil bestaat tussen de gemiddelden.
- De p-waarde (
p-value) geeft aan of het waargenomen verschil tussen de gemiddelden statistisch significant is. - Een p-waarde kleiner dan 0.05 suggereert een verschil.
Met onderstaande code testen we dit met een if-else statement:
p_value <- result$p.value
print(paste("P-value:", p_value))
if (p_value < 0.05) {
print("P-value below 0.05: Significant relation!")
} else {
print("P-value above 0.05: NO siginificant relation!")
}## [1] "P-value below 0.05: Significant relation!"Er is een p-waarde berekend kleiner dan 0.05.
Er is dus een significant verschil tussen score voor, en na het volgen van de opleiding. Het is significant dat de score hoger is na het volgen van de opleiding.
Uitleg en voorbeeld independent t-test
Vergelijkt gemiddelden, van twee niet van elkaar afhankelijke groepen, om verschillen te bepalen. Voorbeeld: Om te bepalen of er verschil is in gemiddelde lichaamslengtes van mannen en vrouwen.
Dataset uitlezen
We gebruiken een dataset met lichaamslengtes van mannen en vrouwen. Hiervan is te verwachten dat de lengtes normaal verdeeld zullen zijn. We gaan met een independent t-test bepalen of er significant verschil is in gemiddelde lichaamslengtes.
df_body_lengths <- data.frame(
lengths_females = c(155.5, 160.2, 160.5, 162.6, 165.1, 156.3, 164.5, 163.7, 157.9, 160.7),
lengts_males = c(168.3, 181.2, 174.8, 167.7, 170.4, 169.9, 170.7, 182.5, 165.8, 179.6)
)
df_body_lengths## lengths_females lengts_males
## 1 155.5 168.3
## 2 160.2 181.2
## 3 160.5 174.8
## 4 162.6 167.7
## 5 165.1 170.4
## 6 156.3 169.9
## 7 164.5 170.7
## 8 163.7 182.5
## 9 157.9 165.8
## 10 160.7 179.6Gemiddelden berekenen
Met de sapply() en mean functies bekijken we alvast de gemiddelde lengte per geslacht:
sapply(X = df_body_lengths, FUN = mean)## lengths_females lengts_males
## 160.70 173.09Berekenen van independent t-test
We zien een verschil tussen de gemiddelde lengtes.
Met de independent t-test kunnen we bepalen of dit verschil significant is.
- Hiervoor gebruiken we de
t.test()functie. - Met argument
var.equal = TRUE.
result <- t.test(
x = df_body_lengths$lengths_females,
y = df_body_lengths$lengths_males,
var.equal = TRUE
)
result##
## One Sample t-test
##
## data: df_body_lengths$lengths_females
## t = 151.74, df = 9, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 158.3043 163.0957
## sample estimates:
## mean of x
## 160.7Interpretatie van resultaten
In de resultaten zien we een p-waarde kleiner dan 0.05.
Dit betekent dat het verschil in gemiddelde lengtes significant is.
Expert worden in data-analyse & statistiek met R?
Wil jij goed leren werken in R? Tijdens onze Opleiding R leer je alles wat je nodig hebt om zelfstandig analyses uit te voeren in R. In deze opleiding kun je kiezen voor een extra dag waarin je alles leert over statistiek met R.

Rik is data scientist en marketeer bij Data Science Partners. Vanuit zijn achtergrond op de Technische Universiteit Eindhoven heeft hij veel affiniteit met data. Na zijn studie heeft hij als consultant altijd met data gewerkt en tevens ervaring opgedaan in het geven van trainingen.