Logistic Regression in R: uitleg hoe je dat doet incl. voorbeeld

In dit blog gaan we in op hoe je een logistic regression uitvoert in R. We illustreren dit aan de hand van een voorbeeld.

Inhoud van dit blog

• Lineaire regressie vs. logistische regressie
• Logistic regression stap 1: data uitlezen
• Logistic regression stap 2: aannames
• Logistic regression stap 3: scatterplot
• Logistic regression stap 4: uitvoeren logistische regressie
• Logistic regression stap 5: interpreteren resultaten
• Logistic regression stap 6: visualisatie resultaat

Lineaire regressie vs. logistische regressie

Logistic regression behoort tot de methoden die worden gebruikt om toekomstige uitkomsten te voorspellen op basis van beschikbare gegevens. Dit doe je door het samenstellen van een model. Met behulp van statistiek is de kracht/bruikbaarheid van een model te beoordelen.

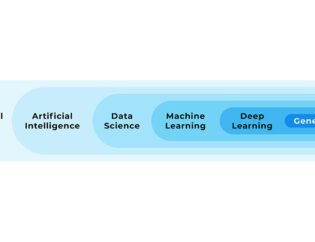
In onderstaande afbeelding kun je zien welke plaats logistic regression inneemt tussen andere statistische algoritmes.

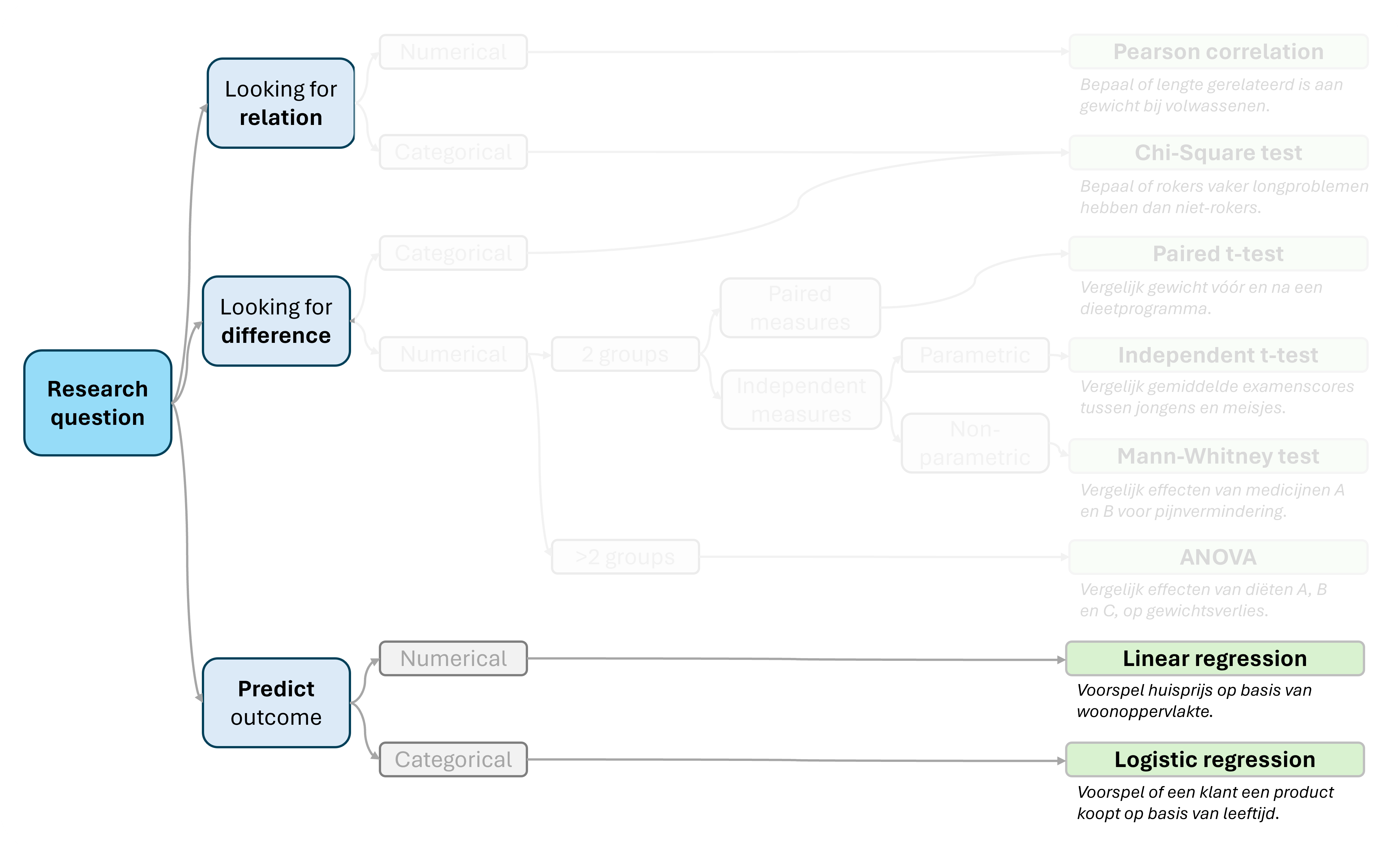
• Logistische regressie is een statistische techniek die wordt gebruikt om de kans te voorspellen van een binair resultaat (bijvoorbeeld ja/nee, geslaagd/ongeslaagd), op basis van één of meer voorspellende variabelen. Het model berekent de kans op een bepaald resultaat met behulp van een logistische functie. Denk hierbij bijvoorbeeld aan het voorspellen of een hartaandoening zich ontwikkelt. Op basis van risicofactoren zoals leeftijd, geslacht, BMI, bloeddruk, cholesterol-niveaus.
• Lineaire regressie is een statistische methode om de relatie tussen een afhankelijke variabele (uitkomst) en één of meer onafhankelijke variabelen (voorspellers) te onderzoeken. Het doel is om een lineair model te vinden dat de relatie tussen variabelen beschrijft. Bijvoorbeeld het modelleren van de relatie tussen reclame-uitgaven en verkoopcijfers.

In dit artikel gaan we dieper in op logistic regression in R.

Zie ook dit uitgebreide blog over lineaire regressie in R

1. Dataset uitlezen

We gaan een CSV bestand uitlezen met data van een verkoopgegevens van een bedrijf. Hier kun je het bestand downloaden als je mee wilt doen.

Het bevat de volgende kolommen met gegevens van klanten en verkopen:

1. Age: Leeftijd van de klant.

2. Purchased: Heeft de klant het artikel gekocht (0 = nee, 1 = ja).

df_customer_sales <- read.csv("data/customer_sales_data.csv")

We gaan onderzoeken of we het aankoopgedrag kunnen voorspellen op basis van leeftijd.

2. Aannames checken

Enkele aannames voor het gebruik van een eenvoudige logistische regressie:

• Onafhankelijke observaties: Waarnemingen mogen elkaar niet beïnvloeden.
• Lineair verband: Relatie tussen variabelen, en logaritme van kansen van de uitkomst, is rechtlijnig.

3. Visualiseren met scatterplot

Met een scatterplot (puntenwolk) kunnen we de datapunten visualiseren.

We gebruiken package ggplot2 en functie geom_point():

library(ggplot2)

ggplot(
  data = df_customer_sales,
  aes(x = Age, y = Purchased)
) +
  geom_point(alpha = 0.05, size = 3) +
  labs(
    x = "Age",
    y = "Purchased",
    title = "Age versus Purchased"
  )

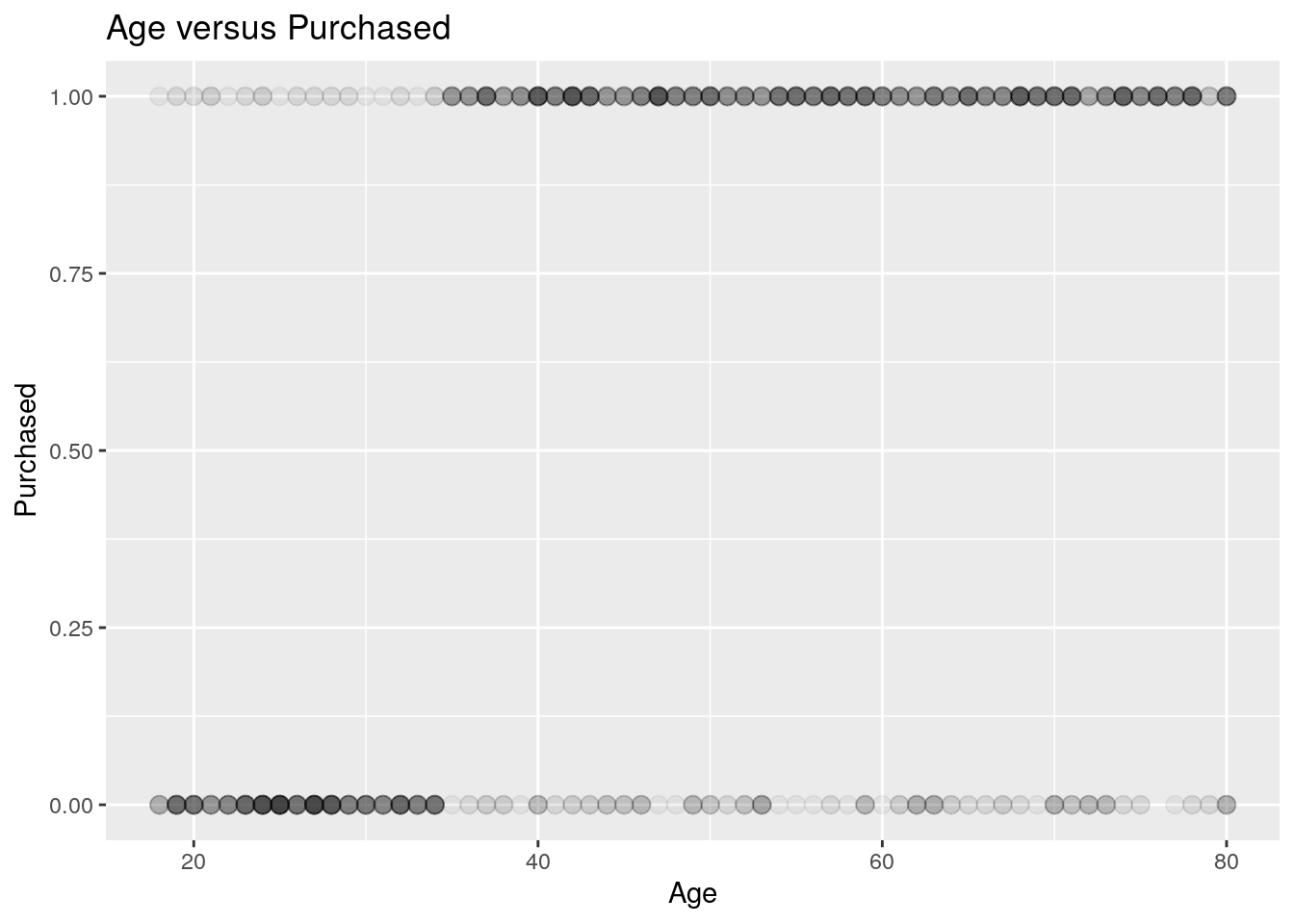
Grafisch is een relatie te zien: Hoe hoger de leeftijd, hoe hoger de kans op een aankoop.

4. Uitvoeren van logistische regressie

Nu we onze data hebben geladen, kunnen we de logistische regressie uitvoeren.

Dit met behulp van de standaard functie glm() (Generalized Linear Model).

• Met formula = Purchased ~ Age geven we de relatie tussen kolommen op.
• Met family = "binomial" zorgen we ervoor dat logistische regressie wordt toegepast.
• Met functie summary() verkrijgen we de uitkomsten van de regressie.

set.seed(123)

logit_model <- glm(
  formula = Purchased ~ Age,
  data = df_customer_sales,
  family = "binomial"
)

summary(logit_model)

## 
## Call:
## glm(formula = Purchased ~ Age, family = "binomial", data = df_customer_sales)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.3992  -0.8348   0.4600   0.8372   1.8457  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -2.757243   0.227627  -12.11   <2e-16 ***
## Age          0.069718   0.004868   14.32   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1332.9  on 999  degrees of freedom
## Residual deviance: 1056.4  on 998  degrees of freedom
## AIC: 1060.4
## 
## Number of Fisher Scoring iterations: 4

De uitvoer bevat informatie over het regressiemodel, waaronder:

• Coëfficiënten van de logistische vergelijking van het model.
• p-waarden voor significantie van de coëfficiënten.

5. Interpretatie van resultaten

Beide coëfficiënten hebben een p-waarde kleiner dan 0.05, en zijn hierdoor significant.

Uitkomsten voorspellen

Laten we nu beoordelen hoe goed het model gemiddeld presteert:

• Aan onze dataset voegen we een kolom toe met voorspellingen van het model.
• Hiervoor gebruiken we de predict() functie. Je gebruikt type = "response" voor voorspellingen van een logistisch-regressie-model. Dit heeft voorspelde kansen, in plaats van logistische waarden.

df_customer_sales$Purchased_predicted <- predict(logit_model, type = "response")

De kolom Purchased_predicted bevat nu de voorspelde kans op een succesvolle aankoop.

Omzetten voorspelde kansen naar binaire waarden

Met een if-else-statement vervangen we de kans door een 0 of 1.

• Met de ifelse() functie. 1 indien voorspelde kans groter dan 0.5, anders 0.

df_customer_sales$Purchased_predicted <- ifelse(
  test = df_customer_sales$Purchased_predicted > 0.5,
  yes = 1,
  no = 0
)

We kunnen nu al visueel de overeenkomsten en verschillen tussen werkelijke en voorspelde uitkomsten zien.

Nauwkeurigheid model

We berekenen nu de nauwkeurigheid van het model.

• Hiervoor gebruiken we de mean() functie.
• Waar we het gemiddelde berekenen van als voorspelling gelijk is aan werkelijkheid: df_customer_sales$Purchased_predicted == df_customer_sales$Purchased

mean(df_customer_sales$Purchased_predicted == df_customer_sales$Purchased)

## [1] 0.793

We zien dat het model ongeveer 4 van de 5 keer correct voorspelt.

Confusion matrix

In een confusion matrix zien we hoe vaak een voorspelling goed of fout gaat.

• Hiervoor is de table() functie te gebruiken.
• We geven voorspellingen en werkelijke waarden op.

conf_matrix <- table(df_customer_sales$Purchased, df_customer_sales$Purchased_predicted)

conf_matrix

##    
##       0   1
##   0 260 125
##   1  82 533

De voorspelde waarden staan in de rijen.

De werkelijke waarden in de kolommen.

Voorbeeld: 0 voorspeld, en ook werkelijk 0: 260 keer.

Met de prop.table() functie kunnen we ook de proporties (percentages) tonen:

prop.table(table(df_customer_sales$Purchased, df_customer_sales$Purchased_predicted))

##    
##         0     1
##   0 0.260 0.125
##   1 0.082 0.533

6. Visualiseren van voorspellingen

We kunnen aan de eerder gemaakte scatterplot voorspellingsuitkomsten van het model toevoegen.

• Dit doen we met een lijn met geom_line().
• Daarbij gebruiken we de predict() functie om voorspellingen van het model te verkrijgen.

library(ggplot2)

ggplot(
  data = df_customer_sales,
  aes(x = Age, y = Purchased)
) +
  geom_point(alpha = 0.05, size = 3) +
  geom_line(
    aes(x = Age, y = predict(logit_model, type = "response")),
  color = "blue",
  ) +
  labs(
    x = "Age",
    y = "Purchased",
    title = "Age versus Purchased"
  )

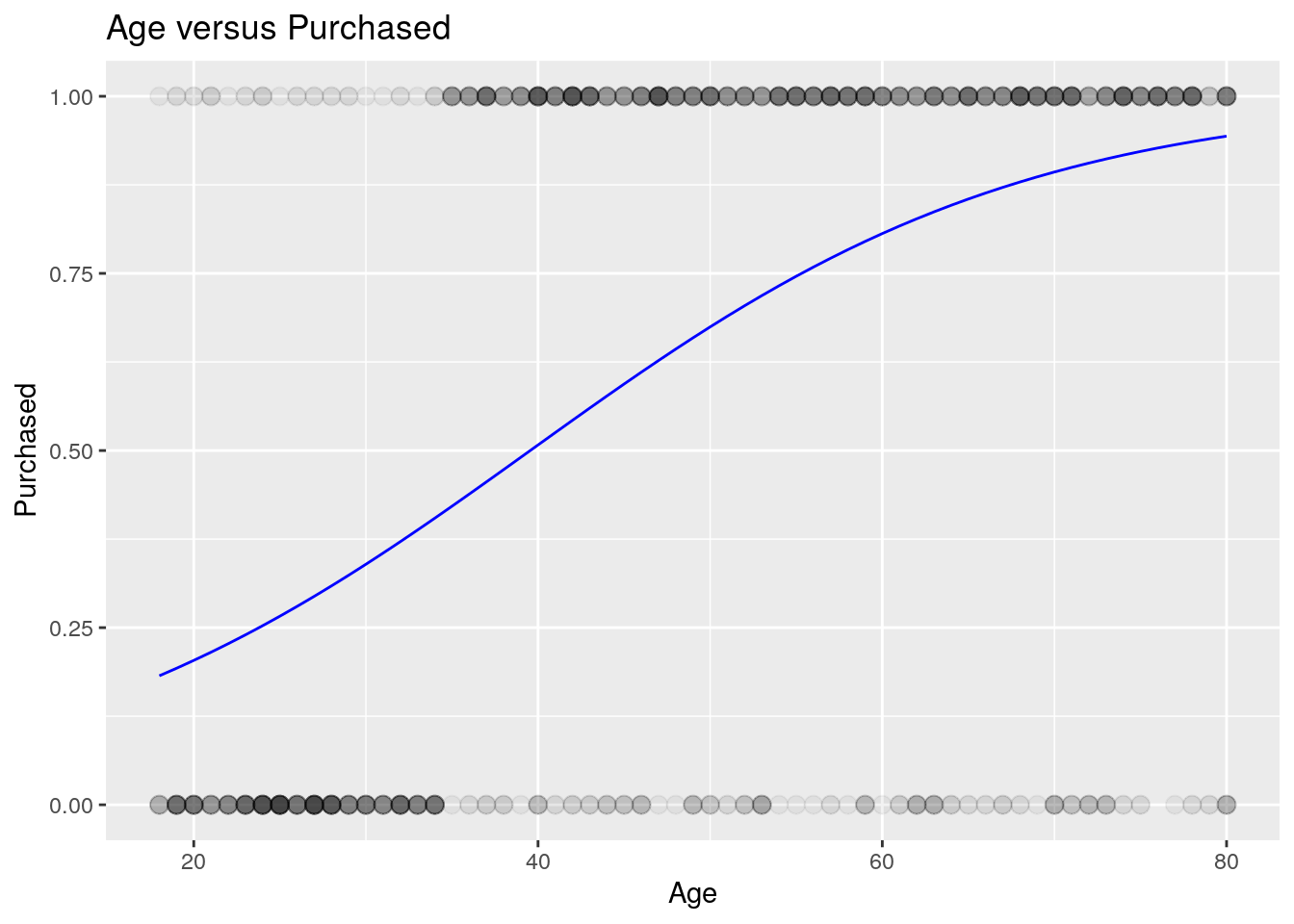
Hierin kun je goed zien dat naarmate de leeftijd toeneemt, de voorspelde kans groter wordt.

Dit blog is onderdeel van onze blogreeks over programmeren in R, de veelzijdige programmeertaal die essentieel is in data science. Of je nu een beginner bent of een ervaren gebruiker, deze serie biedt inzichten en praktische tips voor iedereen. We verkennen de basis met Wat is R? en R installeren, duiken in data manipulatie met dplyr en Data Table package, en onthullen de kracht van visualisatie met ggplot2. Voor een geïntegreerde ontwikkelomgeving, bekijk RStudio, en ontdek hoe R Jupyter Notebook de interactieve programmering verbetert. Verdiep je in de Tidyverse met Tidyverse R en leer over R scripts. Of je nu worstelt met de vraag Is programmeren in R moeilijk?, deze serie heeft voor elk wat wils.

Wil je in 2 of 3 dagen zelfstandig met R leren werken in RStudio?

Wil jij goed leren werken in R? Tijdens onze Opleiding R leer je alles wat je nodig hebt om zelfstandig analyses uit te voeren in R. In deze opleiding kun je kiezen voor een extra dag waarin je alles leert over statistiek met R.