Mann-Whitney test in R: Wat is het, hoe werkt het, en voorbeelden

In deze blog laten we zien hoe je de Mann-Whitney test uitvoert in R. We leggen kort uit wanneer je deze statistische test toepast en tonen aan de hand van een voorbeeld hoe je de test toepast in R.

Als je mee wilt doen met deze tutorial moet je R installeren en RStudio installeren.

We behandelen de volgende onderwerpen:

• Wat is de Mann-Whitney test en wanneer gebruik je het?
• Stap 1: Dataset uitlezen
• Stap 2: Aannames
• Stap 3: Testen van data: niet normaal verdeeld
• Stap 4: Medianen berekenen
• Stap 5: Visualiseren van data met boxplot
• Stap 6: Uitvoeren van Mann-Whitney test
• Stap 7: Interpretatie van resultaten

Wat is de Mann-Whitney test en wanneer gebruik je het?

De Mann-Whitney test is een niet-parametrische statistische test die gebruikt wordt om te bepalen of er een significant verschil is tussen twee onafhankelijke groepen op basis van rangorde van data. Dit betekent dat je de test gebruikt om te bepalen of er een verschil is in numerieke waarden van 2 groepen, die geen invloed hebben op elkaar, waarbij de data niet normaal verdeeld is. Daarbij worden de medianen vergeleken. Wanneer de data wel normaal verdeeld is, kun je een onafhankelijke t-test gebruiken.

Voorbeeld van gebruik Mann-Whitney test: Om te bepalen of er verschil is in pijnbestrijding van 2 verschillende soorten medicijnen.

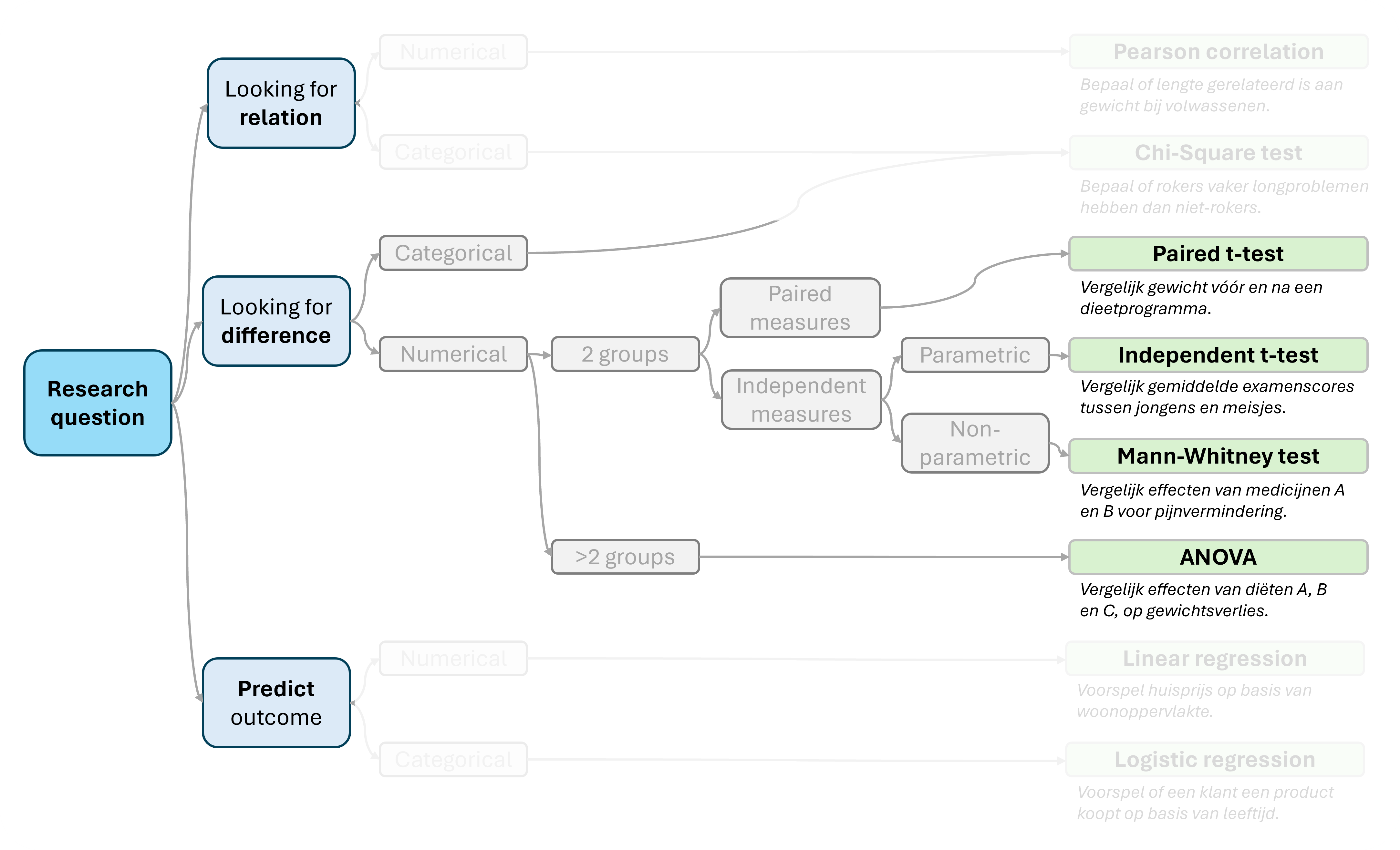
We zullen nu stap voor stap laten zien hoe je de Mann-Whitney test uitvoert en interpreteert in R.

Stap 1: Dataset uitlezen

We gaan in het voorbeeld aan de slag met data van van 2 verschillende medicijnen die pijn bestrijden: medicijn A en medicijn B. Elk van de medicijnen is door een andere groep van 50 patiënten gebruikt, en zij hebben na gebruik de effectiviteit een cijfer gegeven. We bewaren de cijfers in 2 vectoren.

scores_medicine_a <- c(
  3, 6, 7, 6, 5, 5, 3, 4, 8, 4,
  4, 3, 8, 7, 8, 5, 4, 5, 5, 5,
  8, 3, 5, 5, 7, 4, 5, 5, 3, 5,
  3, 3, 5, 6, 4, 7, 5, 8, 2, 5,
  6, 3, 3, 5, 7, 5, 5, 4, 4, 4)

scores_medicine_b <- c(
  6, 6, 8, 6, 7, 8, 8, 6, 6, 7,
  9, 6, 8, 8, 8, 7, 8, 7, 6, 6,
  8, 8, 6, 8, 9, 8, 8, 7, 6, 7,
  6, 9, 5, 6, 7, 6, 8, 5, 8, 7,
  6, 8, 9, 6, 7, 7, 8, 7, 9, 7)

Stap 2: Aannames

Er zijn enkele aannames van toepassing voor het gebruik van een Mann-Whitney test:

• De observaties in elke groep zijn onafhankelijk van elkaar.
• De meetniveaus van de variabelen zijn minstens ordinaal.
• De verdeling van de scores binnen elke groep is vergelijkbaar en niet normaal verdeeld.

Stap 3: Testen van data: niet normaal verdeeld

Eén van de aannames is dat de data in de datasets niet normaal verdeeld zijn. Dit kunnen we testen. Hiervoor gebruiken we de Shapiro-Wilk test.

Dit doen we met onderstaande code voor beide datasets:

shapiro.test(scores_medicine_a)
shapiro.test(scores_medicine_b)

Output:
    Shapiro-Wilk normality test

data:  scores_medicine_a
W = 0.91874, p-value = 0.002123

    Shapiro-Wilk normality test

data:  scores_medicine_b
W = 0.89762, p-value = 0.0004013

In de output is te zien dat beide tests een p-waarde kleiner dan 0.05 opleveren. Dit betekent dat beide datasets niet normaal verdeeld zijn.

Stap 4: Medianen berekenen

We kunnen met onderstaande code voor beide groepen de medianen berekenen:

median(scores_medicine_a)
median(scores_medicine_b)

Output:
[1] 5
[1] 7

Hier is te zien dat medicijn B een hogere mediaan heeft. We gaan met de Mann-Whitney test onderzoeken of dit ook werkelijk een significant hogere waarde is dan van medicijn A.

Stap 5: Visualiseren van data met boxplot

Je kunt de scores voor beide medicijnen goed visualiseren in een boxplot. Dit doen we in onderstaande code.

boxplot(scores_medicine_a, scores_medicine_b,
  names = c("Medicine A", "Medicine B"),
  main = "Boxplot of scores for medicine A and medicine B",
  ylab = "Score",
  col = c("skyblue", "grey"))

Output: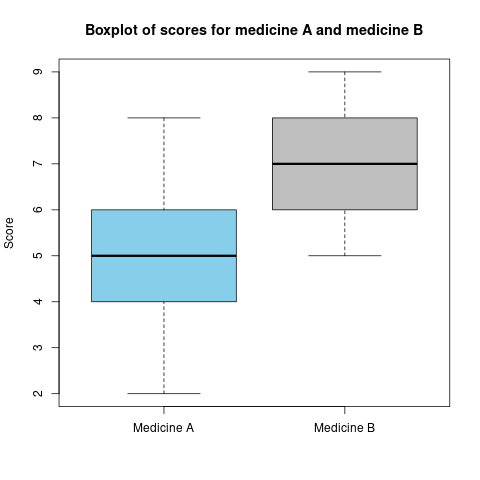

Je kunt hier goed diverse verschillen in zien tussen scores van medicijn A en B.

Stap 6: Uitvoeren van Mann-Whitney test

Nu we weten dat beide datasets niet normaal verdeeld zijn, en we hebben gezien dat er een verschil is in medianen, kunnen we de Mann-Whitney test gaan toepassen. Dit om te bepalen of het verschil in medianen significant is.

Hiervoor gebruik je in R de wilcox.test() functie. Hiermee kan zowel de Mann-Whitney test als de Wilcoxon signed rank toets uitgevoerd worden.

We passen het als volgt toe:

test_result <- wilcox.test(scores_medicine_a, scores_medicine_b)

test_result

Output:
    Wilcoxon rank sum test with continuity correction

data:  scores_medicine_a and scores_medicine_b
W = 355, p-value = 3.871e-10
alternative hypothesis: true location shift is not equal to 0

Stap 7: Interpretatie van resultaten

We zien in het resultaat een p-waarde kleiner dan 0.05. Dat betekent dat er een significant verschil is. Hierdoor kunnen we de conclusie trekken dat medicijn B gemiddeld gezien een hogere score krijgt dan medicijn A.

Conclusie

We hebbben met een voorbeeld de Mann-Whitney test toegepast in R. Daarbij hebben we datasets op normale verdeling getest met de shapiro.test() functie. Vervolgens hebben we medianen berekend en data gevisualiseerd met een boxplot. Met de wilcox.test() functie hebben we de Mann-Whitney test uitgevoerd. We gebruikten deze statistische test om een verschil aan te tonen in de scores van 2 onfhankelijke groepen, waarbij data niet normaal verdeeld is.

Wil jij goed leren werken in R? En wil je alles leren over statistische analyses met R? Tijdens onze Opleiding R leer je alles wat je nodig hebt om zelfstandig aan de slag te kunnen.